
NASA GPM precipitation retrievals
Building upon the heritage of the Tropical Rainfall Measurement Mission (TRMM), the international Global Precipitation Measurement (GPM) program aims at providing knowledge and data on rain and snow all over the globe for both climate science and operational weather prediction. The GPM Core Observatory satellite is the NASA-JAXA contribution to the GPM program. The GPM Core observatory boards a dual-frequency precipitation radar (DPR) and a passive microwave imager (GMI).
Improving GPM passive microwave precipitation retrieval using pattern information
While the DPR is the only precipitation radar in orbit, several other instruments similar to GMI, integrated into the GPM constellation provide frequent measurements of the microwave radiances at the top of the atmosphere. These radiances are the product of the surface emission, emission and absorption by liquid rain drops and scattering by ice particles in the atmosphere (Figure 1). They are converted into brightness temperature for physical interpretation.
My work focuses on improving the algorithms performing the inversion of the multispectral signatures measured by microwave imagers into hydrometeor profiles. The current operational algorithms, such as the NASA algorithm GPROF, perform the retrieval at the “pixel” level; meaning that they retrieve the hydrometeor profile at a given location (i.e. in a pixel of about 10x10 km) using only the spectral measurements at this location, and ignoring the surrounding observations and the spatial-temporal dynamics of the measured signal. On the contrary, our proposed “nonlocal” retrieval approach utilizes the pattern information and the spatial dynamics of the observed fields of brightness temperature.
The easiest way to extract patterns and spatial dynamics from the 2D fields of brightness temperature is to use convolution filters (Figure 2). When added to the observation vector to create enriched spectral signatures, the nonlocal parameters extracted by the convolution filters help to better constrain the inversion problem and reduce the uncertainty in the retrieval of hydrometeor profiles and surface precipitation rates (Figure 3). There is potentially an infinite number of nonlocal parameters which can be computed, the challenge of my research is to determine a small number of parameters providing useful information on precipitation.

Figure 1: Principle of the observation of precipitation from passive microwave imagers. The measured spectral signature is the product of the surface emission, emission and absorption by liquid rain drops and scattering by ice particles in the atmosphere.

Figure 2: Using a convolution kernel to extract dynamic and patterns from the field of brightness temperature. (a) First derivative of Gaussian kernel. (b) Brightness temperature field at 89 GHz observed by GMI. (c) Result of the convolution of (b) with (a). Here the extracted information is the spatial derivative of the field along the imager’s observation direction.

Figure 3: Mean absolute error of the retrieved near-surface precipitation rate over land as a function of the number k of neighbors when using a nearest-neighbor algorithm with and without using nonlocal parameters. Here only three nonlocal parameters are used. The k-nearest-neighbor algorithm relies on a database of 700 000 collocated radar profiles and GMI spectral signatures.
Using patterns and multiscale representations to compare and validate precipitation estimates.
Another part of our work focuses on the comparison and evaluation of precipitation products. As for the retrieval, the comparison of precipitation products is classically performed at the pixel level. This pixel-to-pixel approach can be limiting in some aspects, in particular it is weak at assessing mislocation errors and at quantifying the dependence of the retrieval performances to spatial and temporal scales. Among the commonly used tools to analyses physical fields are the spectral transforms (e.g. Fourier, wavelets, discrete cosines) obtained by convolving the field with a basis of elemental functions. High-value spectral coefficients are obtained when the features in the field match one of these elemental functions, making the spectral representations useful for feature/pattern extraction. The spectral transforms are in particular a potent tool to analyze spatial-temporal dynamical modes and couplings in precipitation datasets (Figure 4). Additionally, the spectral approach allows us to assess the ability of products in reproducing the precipitation patterns as a function of the spatial frequency/scale and to define the “effective resolution” as the finest scale at which minimal performance requirements are met (Figure 5).
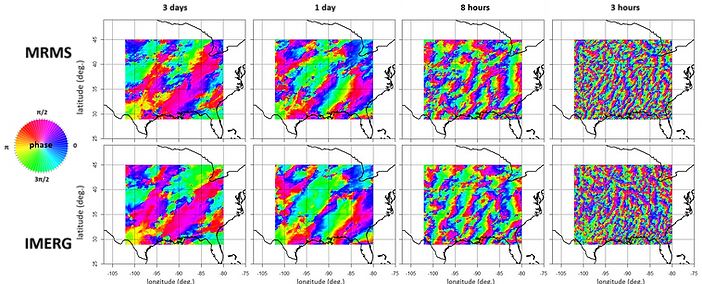
Figure 4: Temporal phase in the Fourier domain of precipitation over the US at 3 days, 1 day, 8 hours and 3 hours periods, from the MRMS gauge-radar product and form the IMERG satellite product for the April-October 2017 period. The phase informs us on the spatial-temporal dynamics and on the propagation of the precipitation systems.

Figure 5: Fourier spectral coherence between the MRMS gauge-radar product and the the IMERG satellite product for the April-October 2017 period over the US as a function of temporal period and spatial wavelength. Assuming that the MRMS product is a good reference, the “effective resolution” of IMERG can be defined as the finest scale at which the squared coherence is higher than 0.5.